Recommendation models

Recommendation models are significantly larger (2x-10x) than large language models, but they are sparse which means they require 1000x fewer FLOPS.¹

In an idealized recommendation model,

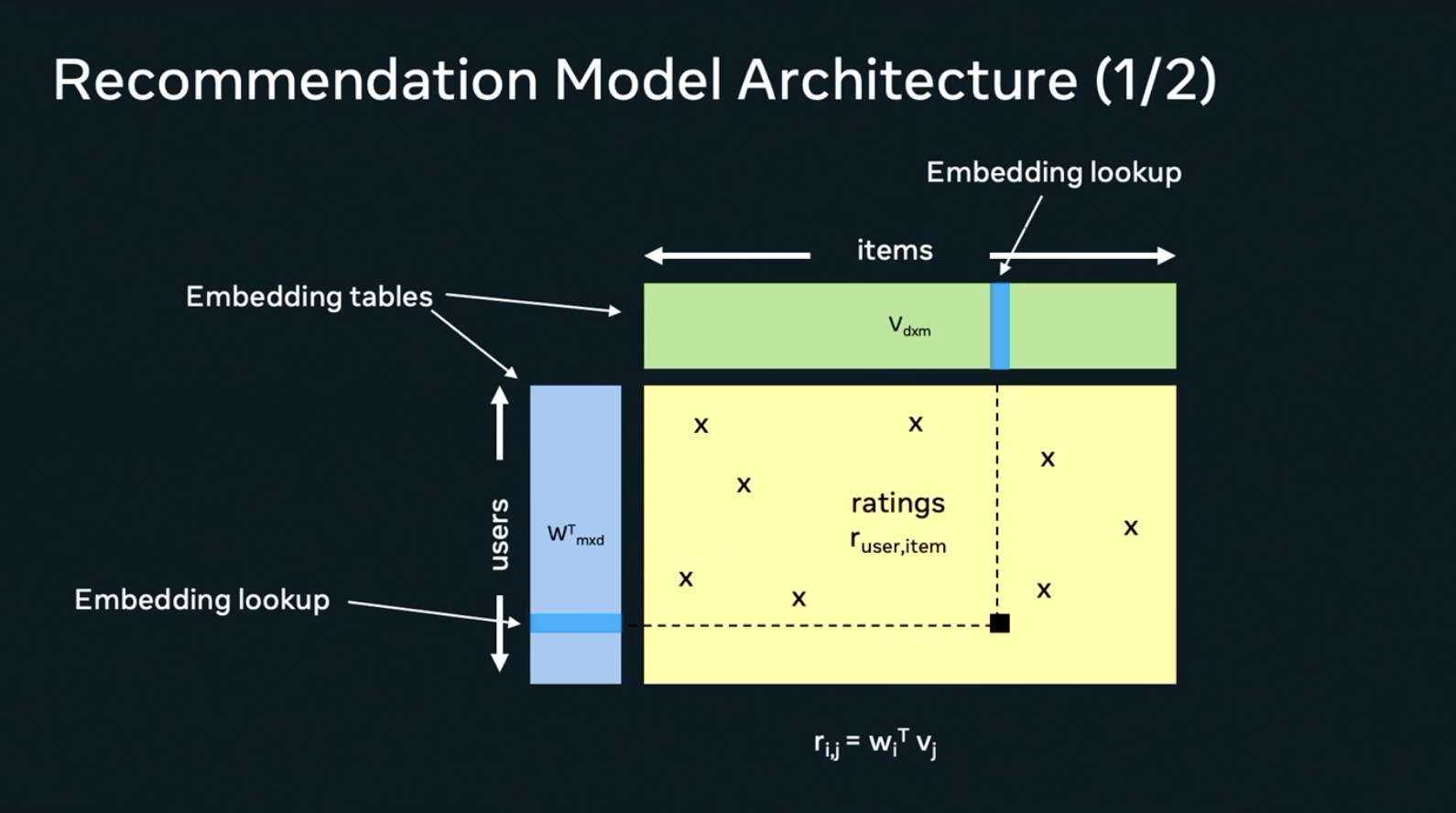
there are notionally three matrices:

• Users, whose components encode different attributes of a user. Its dimensions, $d\times m$, might represent $d$ different users and $m$ different features of each user. There could be billions of users and dozens or hundreds of features.
• Items, whose components represent features of the things that will be recommended.
• Ratings, which are sparse, observed values that reflect the few points where a specific user rated a specific item.

When training a recommender, the goal is to recreate the values of the user and items vectors using whatever information is in the ratings matrix.

Balaji put forth the following example to demonstrate the computational challenges of recommendation training:

• Users may have a billion entries
• Movies may have a million entries

You have to dot product rows and columns at random (termed embedding lookups) which amount to random lookups from a giant embedding table in memory.

Footnotes

1. Balaji, Architectural Challenges in Modern AI Workloads. Workshop on Co-design of Next-Generation HPC Systems for Artificial Intelligence and Mixed Analytics. SC’24. ↩